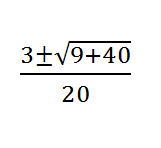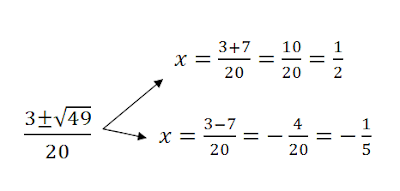FUNCIONES: PUNTOS DE CORTE CON EL EJE X E Y

FUNCIONES: AVERIGUA EL PUNTO DE CORTE CON LOS EJES

Buenas chic@s, hoy os voy a mostrar como localizar en una gráfica los puntos de corte con los ejes "x" e "y" de una función polinómica. Además, aprenderemos a calcularlos a partir de la función dada.

Comencemos por localizar los puntos de corte con los ejes en la siguiente gráfica:

Nuestra gráfica tiene dos líneas, una horizontal llamada eje x y una vertical llamada eje y.

Un punto de corte es aquél en el que la línea de nuestra función atraviesa uno de los ejes.

Si nos fijamos en el eje x, nuestra función atraviesa en el punto -4 y vuelve a atravesar en el punto 2. A la hora de anotarlo lo tenemos que realizar de la siguiente manera:

Puntos de corte con el eje x: (-4,0) y (5,0).

Lo representamos en forma de coordenada donde el primer número corresponde al eje x y el segundo al eje y (x , y). Siempre en el punto de corte con "x" "y" será 0.

Ahora, pasemos a ver el eje y, nuestra función atraviesa el eje en el -8. para anotarlo lo hacemos de igual forma que con el eje x:

Puntos de corte con el eje y: (0,-8).

En los puntos de corte con el eje "y" "x" siempre es 0.

Pasemos ahora a calcular nosotros los puntos de corte de la siguiente función para poder representarla gráficamente:

f(x)= -2x₂ +11x -15

F(x) es nuestra y, para calcular los puntos de corte con el eje x convertimos f(x) en 0 y nos queda una ecuación de segundo grado que al resolverla nos da nuestros puntos de corte con el eje x.

Nuestros puntos con el eje x son: (2,5 , 0) y (3, 0)

Por el contrario, para calcular los puntos de corte con el eje y convertimos las "x" en 0 y nos saldrán nuestros puntos de corte con el eje y.

f(x)= -2 (0)₂ +11 (0) -15 → -15.

Nuestros punto de corte con el eje y sería: (0, -15)



Aquí la explicación en nuestro canal de youtube.

Espero que os haya servido de ayuda, nos vemos pronto por mi baúl de apuntes.

POLINOMIOS: EXTRAE FACTOR COMÚN

POLINOMIOS: CÓMO EXTRAER FACTOR COMÚN

Hola chic@s, hoy os traigo algo básico como es extraer factor común de un polinomio, aunque es relativamente sencillo no podemos dar por hecho que todos sabemos realizar dicha extracción, sobre todo aquellos que están comenzando en el mundo de los polinomios. Es sencillo pero también esencial para realizar mucho de los ejercicios de polinomios.

 Por todo ello os dejo un vídeo de nuestro canal de youtube para que aprendáis o repaséis de forma rápida cómo extraer factores de un polinomio.

Espero que os sirva de ayuda, nos seguimos viendo por mi baúl de apuntes.

ECUACIONES DE SEGUNDO GRADO COMPLETAS: EJERCICIO RESUELTO

ECUACIÓN DE SEGUNDO GRADO COMPLETA: EJERCICIO RESUELTO

Hola chic@s, hacemos un descanso en polinomios para empezar a adentrarnos en las ecuaciones.
Hoy os enseñaré cómo se resuelve una ecuación de segundo grado completa, pero primero necesitamos aprender a identificarla.

Una ecuación de segundo grado completa tiene la siguiente forma: ax² +bx +c =0

Tendremos tres términos, uno de ellos debe ser de grado dos, uno de grado uno y el término independiente, y por supuesto debe estar igualada a 0 para poder llamarla ecuación.

Ecuaciones de segundo grado existen tanto completas (aquellas que tienen los tres términos antes indicados) como incompletas que pueden ser de dos tipos:

1ª tipo: falta el término b: ax² +c= 0.
2º tipo: falta el término c: ax² +bx= 0.

Lo que NUNCA puede faltar es el primer término, el de grado 2, ya que dejaríamos de estar ante una ecuación de segundo grado.

Una vez aclarado esto, hoy nos centraremos en resolver aquellas ecuaciones de segundo grado completas, para ello disponemos de una fórmula que es la siguiente:
Ahora pasaremos a realizar la siguiente ecuación: 10x² -3x -1= 0;

a=10
b=-3
c= -1

Lo primero, sería establecer quien es a, b y c, cogiendo el número con su signo sin la parte literal (la x). Es importante que recordéis que "a" siempre es aquel término de grado 2, "b" será el término de grado 1 y "c" el término independiente. A veces nos pueden aparecer desordenados, es importante que os fijéis bien y yo os recomiendo que si ese es el caso los ordenéis antes de realizar la operación.

Ahora, sólo tenemos que sustituir cada número en su lugar correspondiente y realizar la operación. 

 

Como podéis ver, sólo hemos sustituido cada número en su letra correspondiente y hemos calculado. Al ser de segundo grado tiene que tener 2 resultados la x, por ello al final se desglosa en 2 utilizando en uno de ellos el signo + de detrás del 3 y en el otro el signo -. Al no poder dividir los resultados por el ser numerador más pequeño que el denominador hemos pasado a simplificar el resultado lo máximo posible.

Os dejo el vídeo de nuestro canal de youtube donde podéis encontrar la ecuación paso a paso.

Espero que os haya servido de ayuda y nos seguimos viendo por mi baúl de apuntes.

POLINOMIOS: CALCULA M PARA QUE LA DIVISIÓN SEA EXACTA

POLINOMIOS: CALCULA "M" PARA QUE LA DIVISIÓN SEA EXACTA

Hola chic@s, seguimos con el tema de polinomios y hoy os enseñaré a realizar un ejercicio muy común cuando trabajamos con polinomios, nos piden calcular una incógnita que ya puede llamarse "m" como es el caso o con cualquier otra de las letras del abecedario.

La división que nos dan es la siguiente:

(2x₄ +8x₃ -20x₂ -24x +16m) : (x-2)

En este tipo de ejercicios utilizaremos la división mediante Ruffini, ahí os dejo el enlace a la entrada del blog donde la explicamos con detalle por si alguno está un poco perdido. 

Aqui tenéis el ejercicio resuelto, lo más relevante es que +16m no puede unirse a -32 sería como unir un número con parte literal (con x) con uno que no tiene parte literal, por ello lo dejamos indicado de forma separada en el resto.

A continuación solo tenemos que coger nuestro resto e igualarlo a 0 en este caso porque nos pide en el enunciado que la división sea exacta si pidiese otra cosa lo igualaríamos a lo que nos indique. Ya sólo tenemos que despejar m y tendríamos el ejercicio terminado.

Si os interesa ver el procedimiento en vídeo os dejo el enlace a nuestro canal de youtube.

¡Nos vemos pronto por el blog con más ejercicios!

POLINOMIOS: MULTIPLICA POLINOMIOS PASO A PASO

MULTIPLICA POLINOMIOS

Bienvenidos de nuevo al blog, hoy os mostraré como multiplicar polinomios fácil de dos maneras diferentes, ¿os animáis? 

1ª forma: Multiplicaremos en horizontal, como en toda multiplicación multiplicaremos todos los términos del segundo polinomio por cada uno de los términos del primer polinomio, a continuación, sumaremos los resultados.

Es importante saber que multiplicaremos los números, los signos ( signos diferentes será "-" y signos iguales "+") y sumaremos el grado de las partes literales. Mientras que en la suma y resta solo puedo sumar o restar aquellos con la misma parte literal, en la multiplicación eso no ocurr. Pasemos a verlo en la práctica:

(2x₃ - 3x₂ +4x) ( 2x₂-3) =

Multiplicaremos 2x₂ de nuestro segundo polinomio por todos los términos del primer polinomio:

2x₂ *  2x₃ = +4x₅ ( se han multiplicado los signos y números y sumado los grados de la parte literal)

2x₂ * (-3x₂) = -6x₄

 2x₂* +4x = +8x₃

Ahora haremos lo mismo con el segundo término del polinomio “ -3 ”:

-3* 2x₃= -6x₃

-3* (-3x₂)= +9x₂

-3* +4x = -12x

Ahora colocamos todos los resultados en fila con su signo correspondiente en el orden que los hemos calculado:

(2x₃ - 3x₂ +4x) ( 2x₂-3) = +4x₅ -6x₄ +8x₃ -6x₃ +9x₂ -12x= +4x₅ -6x₄ +2x₃ +9x₂ -12x

Por último, hemos agrupado aquellos con la misma parte literal, teniendo en cuenta que si tienen signos iguales se suma y dejamos el mismo signo y si son diferentes se resta y colocamos el signo del mayor ( esto lo tenéis explicado en detalle en el post de suma y resta de polinomios).

2ª Forma: También podemos realizar la multiplicación de forma vertical, para ello os dejo el siguiente enlace al vídeo de youtube de nuestro canal donde podéis aprender a realizarla ¡No os lo perdáis!

Nos seguimos viendo por mi baúl de apuntes, hasta la próxima.

POLINOMIOS: EL TEOREMA DEL RESTO

EL TEOREMA DEL RESTO

Hoy vamos a aprender para qué se utiliza el teorema del resto cuando trabajamos con polinomios, seguid leyendo que os dejo un ejercicio paso a paso.


La regla nos dice que gracias al teorema del resto podemos saber el resto de una división de polinomios sin realizarla. 

(2x₂ +3x -2) : (x - 2)

Según el teorema del resto cogemos el -2 del divisor y lo sustituimos en todas las x del dividendo con signo contrario, operamos y ya tendremos nuestro resto.

2 (2)₂ +3 (2) -2= 2*4 +6 -2= 12

Ahora realizaremos la división por ruffini, os dejo el enlace al post sobre la regla de ruffini, y comprobaremos que el resultado es el mismo.

Ambos restos dan 12, es una forma de comprobar si hemos realizado bien el ejercicio.

Espero que os haya servido de ayuda, si os quedan dudas os dejo el ⇰ vídeo que está publicado en nuestro canal de youtube sobre el teorema del resto.

Nos seguimos viendo por mi baúl de apuntes.

MATEMÁTICAS: RESTA DE POLINOMIOS

Seguimos trabajando con polinomios. En esta lección veremos la resta de polinomios realizada de dos formas diferentes. 

En el ejercicio nos dan los siguientes polinomios:

P(x)= 2x₃ -3x₂ +4x -2

Q(x)= x₄ –x₃ +3x₂ + 4

Tanto en la suma como en la resta solo podremos sumar o restar aquellos con la misma parte literal.

RESTA DE POLINOMIO:

1ª Forma: Los colocamos en fila cambiando todos los signos del segundo polinomio Q(x) y luego agrupamos los que tengan la misma parte literal:

(2x₃ -3x₂ +4x -2) – (x₄ -x₃ +3x₂+4) = 2x₃ -3x₂ +4x -2 -x₄ +x₃ -3x₂ -4 = -x₄ +3x₃ -6x₂ +4x -6.

Como podéis ver el segundo polinomio ha cambiado todos sus signo para restar, teniendo en cuenta que el signo de restar no aparece por ningún sitio. En resumen, colocamos el primer polinomio exactamente igual y el segundo con todos los signos cambiados, ahora ya podemos agrupar los que tengan la misma parte literal. 

Veámoslo paso a paso:

-x₄ se coloca tal cual ya que no hay ningún otro de grado 4.

De grado 3 tenemos 2x₃ y +x₃ = recordad que como vimos en la lección de suma de polinomios, si tienen el mismo signo sumamos y dejamos el mismo signo= +3x₃. Os recuerdo que los números se suman o restan pero la parte literal no cambia.

De grado 2 tenemos -3x₂ y -3x₂ = como en el caso anterior, al tener el mismo signo sumamos y colocamos el mismo signo: -6x₂.

De grado 1 sólo nos encontramos con +4x, por lo que se coloca tal cual en el resultado.

Por último, sin parte literal tenemos -2 y -4 que al tener el mismo signo se suman y queda -6.

Aclaración: En el caso de que nos aparezcan dos números con la misma parte literal y signos contrarios, restaríamos y dejaríamos el signo del mayor. No ha ocurrido en este caso, pero tenéis ejemplos de ello en la suma de polinomios.

2ª Forma: Colocaremos  un polinomio debajo del otro, el segundo de ellos con todos sus signos cambiados (es la única diferencia con la suma de polinomios) quedando en fila aquellos con la misma parte literal:

Tenéis el ejercicio resuelto en este vídeo.

Aquí termina la lección de hoy, si os ha servido de ayuda seguid por mi baúl de apuntes, nos vemos pronto con más lecciones.